宇宙膨胀背后的故事(十九)
暴胀的宇宙
1979年,正在重新打开国门的中国大陆吸引了大量海外华裔的注意力。戴自海作为最年轻的成员参加了一个由杨振宁和李政道(Tsung-Dao Lee)召集、30位美籍华人物理学家组成的访华团,从年底开始在中国旅行6个星期,访问各地的科研机构。
他们的行程包括1980年1月初在广州市郊区从化温泉举行的一个基本粒子物理讨论会。那是中国文化大革命之后的第一个大规模国际物理会议,有50位来自世界各地的华裔物理学家参加,是中国物理学界与国际重新接轨的一次里程碑意义的盛举。
对于年轻的戴自海来说,他得以重返童年时便离开了的故土,再次见到留在上海、已经许多年未见的奶奶。
古斯对地球另一边的这个时代性变迁没有感觉。他只知道他的合作者要去一个遥远、闭塞的国度,会失去联系近两个月。因此,他们必须在那之前完成论文,以免夜长梦多。
其实,古斯自己几个月前已经离开了康奈尔,横穿美国搬到加州的斯坦福直线加速器国家实验室。那也是戴自海给他出的主意。国家实验室有一年期的博士后资助比较容易申请。在已经有康奈尔三年博士后资助的中间找这么一个机会,可以将博士后生涯再加上一年。同时也可以开阔眼界结交朋友,为找工作增加门路。戴自海自己去康奈尔前就在费米实验室呆过一年,在那里迷上了大统一理论。
位于斯坦福的这个实验室拥有当时世界上威力最强大的加速器,正在开展一系列突破性的研究,是大统一理论的重要实验基地。古斯在这里遇见更多的行家里手,经常一起讨论切磋,受益匪浅。他和戴自海则保持着经常的电话联系,紧锣密鼓地工作着。
直到那年11月底,他们才找到了利用过冷的延迟相变避免磁单极问题的诀窍。戴自海随之好奇:这样的延期相变对宇宙膨胀本身会不会有什么影响?
在宇宙模型上,牛顿和爱因斯坦两位泰斗都曾有过同类的低级失误,把不稳定的数学解当作物理的实际。牛顿以为只要宇宙无限大、星星无穷多就可以相互抵消引力的作用有个稳定的世界。爱因斯坦则把引入宇宙常数后的一个不随时间变化的解作为现实的宇宙。但这两种情形都是不可能真实存在的“不稳定态”。
就像要在陡峭的尖顶上平衡一块巨石,在数学上是可能的。但巨石的势能很大,又没有稳固的支撑,总会自己滚落下来,所以说那是不稳定的。滚落到山脚下后,巨石的势能处于最低状态,不会再自己跑回山上去,因此那才是“稳定态”。一个系统处于不稳定态——如果可能的话——只会是暂时的,它总会自己向稳定态转变。
不过,巨石从不稳定的山顶上向稳定的山底滚落的过程中也可能被山坡上的沟壑、树木等障碍物阻挡而被卡在半山腰,这时它处于一种介于稳定态和不稳定态之间的“亚稳态”(metastable state)。在经典物理中,亚稳态的系统需要外界的帮助获取动能,克服阻挡它的势垒,才能继续走向稳定态——比如有人推动了石头,让它继续滚下山去。
水在摄氏零度以下还没有结冰而进入的过冷状态也是一种亚稳态。一旦有点干扰,这样的水会迅速地结成冰而达到稳定态——发生了延迟的相变。
同样地,当古斯和戴自海为了解决磁单极问题设想让宇宙进入的“过冷”状态也是一个亚稳态。只是,以量子力学为基础的大统一理论有自己的词汇:能量最低的稳定态叫做“真空”,不是真正稳定态的亚稳态则叫做“假真空”(false vacuum)。
亚稳态中的宇宙当然无法指望会有什么人来把它推出来,也不可能有什么外来干扰。但在量子世界中,还有另外克服势垒的套路:宇宙可以通过“隧道效应”直接从假真空过渡到能量最低的真空,那就是当年伽莫夫用来解释原子核衰变的途径。
戴自海好奇的是,宇宙在完成这个相变之前、被“卡”在假真空中的期间,还会“正常”地膨胀吗?
12月6日的晚上,古斯在他妻子和儿子都睡着了之后,照例独自坐到桌前,开始以数学的方式推导这个假真空中的宇宙。
普雷斯基尔已经推算过,如果宇宙经历的是正常的相变,就会产生大量的磁单极。它们的引力作用非常大,能让整个宇宙坍塌。古斯和戴自海的延迟相变则避免了那么多磁单极的出现。
而他们的宇宙进入过冷状态时,也会有新的东西出现:伴随对称性破缺而现身的“希格斯粒子”(Higgs boson)。1古斯非常惊讶地发现在假真空中的希格斯粒子表现得正好与磁单极相反:它们具备负压强,或者说是含有一种不明来历的能量,不仅不会造成宇宙坍塌,反而会推动宇宙急剧般地膨胀:宇宙的大小不再是与时间成正比的匀速增大,而是会呈现指数增长。
说起指数增长,不能不提起印度传说中那个发明国际象棋的大臣向国王索取的报酬:第一个格子里放一粒麦子,第二个两粒,第三个四粒……。不知利害的国王没料到这样的结果会让他倾全国之力也无法满足这个需求。
古斯这个假真空中的宇宙也是同样地增长着:每10⁻³⁷秒的“短暂一刻”相当于棋盘上的一个格子,宇宙的大小会增加一倍。国际象棋的棋盘只有64个格子,大臣索取的麦子数目也就只翻了64番。古斯估算他的宇宙的大小会在总共10⁻³⁵秒的时间内翻100多番,变成比原初10⁵⁰倍。
在“正常”的宇宙大爆炸模型中,这么一点时间内宇宙的大小只会增长10倍。
这时已经是凌晨1点,古斯因为这个结果大为震惊,毫无睡意。
他当即回忆起狄克那个让他印象深刻的讲座。宇宙是否平坦取决于宇宙中物质的密度是否接近于临界密度值,也就是Ω是否接近于1。狄克指出宇宙要有今天的平坦,大爆炸后的一分钟时Ω必须介于0.999999999999999和1.000000000000001之间。似乎只有鬼斧神工才可能这么碰巧。
当宇宙的大小在指数增长时,其密度显然会随之剧烈变化。古斯凭着记忆重复了狄克的演算过程。果然,他发现在他这个新的宇宙里,Ω在指数增长的过程中会急速地趋近于1。因此,在这之前Ω可以是任何数值——无论是成千上万之大,还是几万分之一之小—— 在这么个延迟相变之后、宇宙开始“正常”膨胀过程之际,Ω的数值一定会不大不小,就是1。
因此那不是我们这个宇宙的特别运气,而是延迟相变过程的必然。他几乎是在无意中解决了狄克的难题。今天的宇宙是平坦的,是因为当初有过那么一次指数增长的剧烈“拉伸”,把以前可能有过的任何皱褶、沟壑都给拉平了。
第二天一早,没怎么睡觉的古斯骑自行车直奔办公室。他只用了9分32秒,创下自己的最快纪录(古斯坚持记日记。无论工作、生活,事无巨细均有案可查)。
在查找资料、仔细验算了晚上的推导之后,他在笔记本上写下:“辉煌的领悟”(spectacular realization):超冷可以解释宇宙今天令人难以置信的平坦,因而解决了狄克讲座中的难题。在“解决了”之前他曾写下“可能”(may)二字,稍后又划掉了。
长途电话那头的戴自海却没有反应。狄克讲座的那天,戴自海到得晚,远远地坐在角落里,没有留下什么印象。此时他的心思也不在听他朋友的新发现。他已经在收拾行李准备启程,只希望古斯不要分心,先完成他们的论文再说。
古斯同意不在已经基本完稿的磁单极论文中节外生枝。他们终于在戴自海动身的前一天寄出了论文。电话上道别时,古斯提出他大概不能坐等几个星期,问戴自海是否介意他自己单独来研究、发表这个平坦性问题的解决方案。戴自海还是没能领悟到古斯那番激动背后的重大意义。他们刚刚共同经历过被他人抢先的苦楚。他理解古斯的处境,便不假思索地同意了。
戴自海没料到,在费了九牛二虎之力终于把古斯推上大统一理论的快车之后,自己竟这样错过了一个难得的人生机遇。
古斯没有花费精力去为自己的新发现找一个好名字。也许因为1970年代末的美国正处于经济停滞、通货膨胀失控的泥潭,他把宇宙的这个指数性急速增长的过程就叫做“(通货)膨胀”(inflation)。中文里的“膨胀”(expansion)一词已经被用了,于是把这个新的概念翻译为“暴胀”,意思上倒更为贴切。
戴自海离开之后,古斯在一次午饭时碰巧听到两个同事谈论一篇关于视界问题的论文。那时他对这个困扰天文学界的难题还一无所知。当他搞清楚这个问题——相对方向的微波背景辐射源互相超过了光速可以传播的距离,从来没有机会达成热平衡却处于同一个温度——并回家思考一番之后,不禁哑然失笑。
传统大爆炸理论中的宇宙大小是匀速增长的。我们的视界,也就是我们今天所能看到的宇宙,包含着彼此不在同一个视界中的空间所在。这些地点即使在过去也没有在一个视界之中,因此从来、永远不会有机会互相交流。
但在暴胀理论中,宇宙的大小变化巨大,在暴胀之前只是暴胀后的10⁵⁰分之一,这是一个超越想象能力的比例。他估算我们今天能看到的宇宙之内的所有空间点在暴胀之前都“挤压”在半径只有10⁻⁵²米的、实在是小得可怜的空间里2。那时以光速便可以轻松地抵达这个狭小空间的每一个“角落”。或者说,我们今天的视界,无论是哪个方向上最远的地方,在暴胀之前也都互相包容于同一个视界当中,也就在那时达到过热平衡。
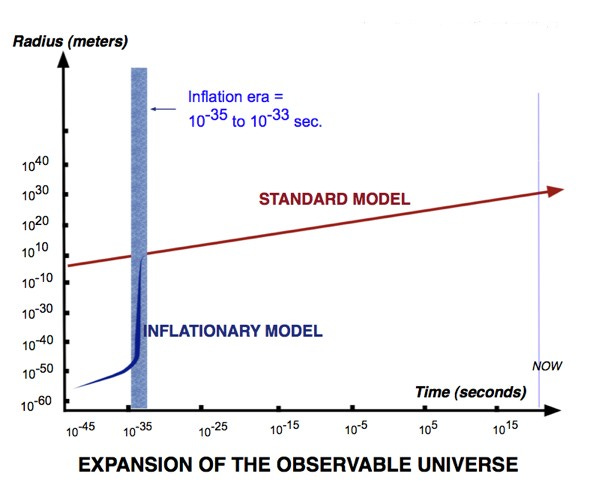
微波辐射出现在大爆炸之后的38万年。那时候宇宙中遥遥相对的两个地点已经彼此离得很远,永久性地失去了联系。虽然它们不可能再“相逢一笑”,但毕竟在“渡尽劫波”的暴胀之前曾是亲兄弟,自然有着同样的物理特性。
于是,暴胀的概念同时解决了大爆炸理论的两大难题,似乎还都“得来全不费工夫”。
1980年1月23日,古斯在实验室举办了一个小讲座,第一次将他的新理论系统地公布于众。他回顾了与戴自海合作的如何用过冷的延迟相变解决磁单极问题,然后指出这个相变导致宇宙的暴胀,可以同时解决宇宙的平坦、视界难题。他连续讲了一个半小时,比通常的讲座时间愣是膨胀了百分之五十。
也正在实验室访问的哈佛大学教授、著名宇宙学家科尔曼(Sidney Coleman)听得津津有味。当古斯事后请教科尔曼如何缩减他讲座的篇幅时,科尔曼竟答曰:“字字珠玑,啥也别删。”3科尔曼随即在他朋友圈子里大力举荐这个新成果。当天,古斯便接到一系列邀请他去讲学的电话。实验室也当即决定将他的博士后资助延长三年。
就在戴自海回美国之际,古斯离开斯坦福,也开始了他一个人长达几个星期的巡回演讲之旅。在一次讲座中,夸克模型的发现者盖尔曼(Murray Gell-Mann)只听了一半便领悟了,禁不住站起来惊呼:“你解决了宇宙学中最重要的问题!”还有人传话,温伯格在听到这个发现时火冒三丈:他气愤的是自己怎么没能想到这个主意。
当然,古斯的收获远远不止于赞赏。在斯坦福的第一次讲座仅仅两天后,他便收到了东部常青藤名校宾夕法尼亚大学招聘他为助理教授的通知。随后,正式的聘请几乎雪片般飞来,其中包括首屈一指的哈佛、普林斯顿等等。他在斟酌比较条件优劣时,突然意识到自己的母校麻省理工学院没有动静。几经犹豫之后,他终于壮起胆子给那里的教授打了电话,结结巴巴地问道:我知道你们今年没有名额,我也就没有申请。不过如果你们愿意……。第二天,麻省理工学院就正式回了话,而且开出了最好的条件:越过助理教授直接聘他为副教授。古斯终于如愿以偿。
旋风般的大半年很快过去了,他还没机会坐下来好好写一篇论文发表。当然他已经不再担心被他人抢先,暴胀理论和他的名字早已一起口口相传。但他这时也有了更深一层的忧虑。当他终于动笔时,论文的标题是《暴胀宇宙:视界和平坦问题的一个可能解决方案》4。
那“可能”二字的再度出现并不完全是谨慎,也是他不得不面对的现实:他这个让整个学术领域兴奋无比的新理论其实存在着可能是致命的缺陷,也许压根就不靠谱。
当一罐水开始结冰时,水中不同的区域会各自开始结晶,形成一个又一个分立的冰泡泡。这些泡泡慢慢增大,互相碰到一起时合并,直到所有的泡泡都融合为一体。这时所有的水都结成了冰,便完成了相变。水在摄氏100度时转化为气态时水中会产生大量的气泡而沸腾。这个相变过程比结冰时的泡泡更为直观。除了相变温度的方向不同,机理是一致的。
宇宙的大统一对称自发破缺时的相变与水结冰过程类似。古斯设想宇宙在通过隧道效应开始其延迟的相变时,也会有很多大大小小的稳定态(真空)泡泡在亚稳态的希格斯场中出现,它们像水中的泡泡一样各自增大后相遇、合并。当所有的泡泡都合并成一个整体的稳定态时,相变——暴胀——便结束了。
在这个过程中,那些泡泡在碰撞、合并时所释放的能量转化为有质量的粒子和反粒子,正好便是温伯格在《最初三分钟》中所描述的大爆炸过程所需要的初始条件。只是现在他知道这时的宇宙密度参数Ω严格等于1,而且视界中的所有空间点都已经处于热平衡。
这一切在古斯最初的演算中合丝合扣,无懈可击。只是他忽视了自己发现的宇宙暴胀本身却也在同时破坏着这个过程的顺利完成。
相变中的泡泡是随机分布的。当泡泡相互合并产生粒子时,这些粒子会集中在泡泡碰撞的地点,在整个空间中并不均匀。古斯设想的是,泡泡们的碰撞会发生得非常地快,产生的粒子再度快速地互相碰撞、散射,立即就会弥漫于整个宇宙空间,不再有不均匀的痕迹。
问题是,在泡泡们碰撞的同时,宇宙本身在暴胀。泡泡之间的距离因而在急速地拉长而失去接触。这样,泡泡碰撞产生的粒子也没时间、机会再重新恢复均匀(也就是热平衡),而应该在空间分布上留有明显的差异。这与今天对微波背景辐射观察的结果不符。
这个结果颇有讽刺意味。古斯在成功地用暴胀解释了我们视界中的宇宙为什么处于热平衡的老问题之后,却又因为暴胀带来了宇宙其实不应该处于热平衡的新问题。
这还不是最糟糕的。暴胀的宇宙大小呈指数式增长。与那位大臣棋盘上的麦子一样,这是难以想象的速度。自然,这个膨胀的速度很快会超过光速。这本身并不是问题,因为宇宙空间的膨胀不传递物理信息,即使速度超光速也没有违背相对论。但空间中的泡泡的增大却是物质、能量的运动,不可能超光速。因此相变中的泡泡增长的速度会远远落后于空间的膨胀速度,以至于泡泡之间的距离会愈来愈大,永远也不可能全部碰到一起合并。这样的宇宙会永久性地布满了众多的泡泡,无法完成相变,无法停止暴胀,永远地被“卡”在一个假真空里。
这既不是古斯的初衷,也不是今天的现实。
古斯直到1980年的8月份才写完这篇论文,次年1月正式发表。他在阐述暴胀宇宙如何解决大爆炸理论两大难题的同时,也一再指出这个新理论自身附带着一些“不可接受的后果”。他不得不为自己发表这个结果找理由:一个能同时解决磁单极、视界、平坦三大难题的新思路——即使结果颇为荒谬——也值得引起更多读者的注意。最后,他希望能有人据此发现某种新途径,“取其精华,去其糟粕”5,解救他的暴胀理论。
私下里,他长出一口气。好在麻省理工学院的工作合同已经签定,他至少有足够的时间再慢慢想办法,暂时不需要担心生计和前途。
他的运气也不错,期盼中的救星很快就出现了。这个好消息也来自地球的另一边。不是开放中的中国,而是还在铁幕后的苏联。
(待续)
物理学家还要等近40年才能在实验中证实希格斯粒子的存在,但在理论上他们并不存疑。
相比之下,(那时还不存在的)质子的半径约为10⁻¹⁵米。
Nothing; every word was pure gold.
Inflationary universe: A possible solution to the horizon and flatness problems
avoids these undesirable features but maintains the desirable ones.