气候变迁背后的故事(十六)
地与月
欧拉赢得的1738年法国科学院大奖是他等待了十一年的殊荣。他在1727年得到博士学位后第一次参加征文比赛,不敌后来被誉为船舶设计之父的法国数学家布格(Pierre Bouguer)。那年的题目是论证桅杆在航船上的最佳位置。刚满二十岁的欧拉还只见过巴塞尔城内莱茵河中的小船。
也是在那个夏天,欧拉搭船顺莱茵河北上,再经陆路到德国的海港。那里有桅杆高耸的海船,将他带往圣彼得堡。十五年前,彼得大帝(Peter the Great)在俄罗斯面向欧洲的出海口创建这座城市并定作首都,体现他引领古老国度“西化”的雄心。彼得堡追崇巴黎的时尚和文化,也在1724年仿照法国科学院成立圣彼得堡科学院。彼得大帝不远万里从欧洲请来几位名家担纲,包括伯努利的两个儿子。大儿子在那里因病早逝后,二儿子丹尼尔·伯努利(Daniel Bernoulli)立即引荐欧拉前来接班。
伯努利是欧洲最著名的数学家,也是欧拉十三岁进入巴塞尔大学时的导师。伯努利一家人才辈出,哥哥和自己的三个儿子都在数学界名声远扬。欧拉的父亲当年在巴塞尔大学时借住在伯努利家里,与未来大师既室友又同学,一起听过伯努利长兄的课。欧拉自己也与伯努利的儿子们结为好友,在毕业后没能在瑞士谋得教职时追随丹尼尔·伯努利远走谋生。丹尼尔·伯努利在1733年回巴塞尔时,年轻的欧拉选择独自留在圣彼得堡继任他的席位。五年后,欧拉摘取法国科学院大奖桂冠,也一举成名。
那年,莫佩尔图亲自带领的远征队完成在北极圈内测量地球的纬度间距后凯旋,带回地球如牛顿所言是一个扁球体的证据。他们测得的数值也与牛顿的预测有偏差。欧拉仔细分析后找出症结所在:牛顿简单地将地球看作一个均匀球体。如果合理地假设地球内部的密度随深度逐渐增大,就能推导出与测量所得相符的尺寸。
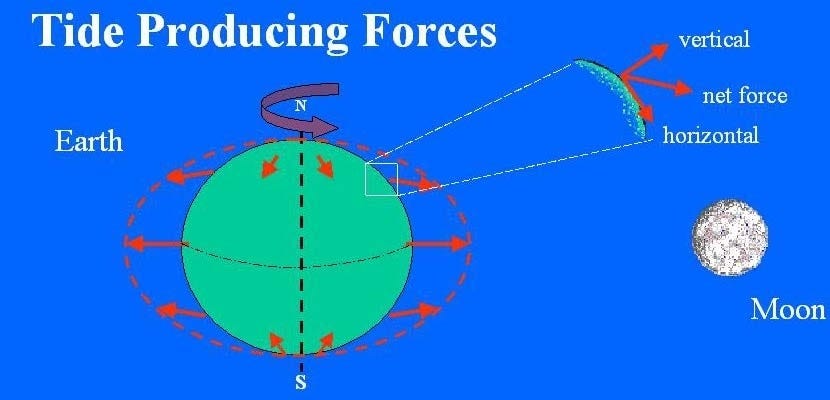
两年后,欧拉又赢得法国科学院1740年的大奖,再次纠正牛顿的失误。那年的题目是海水的运动。五十多年前,牛顿在《自然哲学的数学原理》里以月球和太阳的引力解释地球上潮汐的由来。欧拉在提交的论文里指出牛顿的思路固然正确,具体论证却不成立。月球和太阳的引力在地球的表面远远小于地球自身的引力,不可能如牛顿所述直接在地球与月球或太阳的连线方向上拉动海水而成海潮。但在与该连线有偏角的侧面,月球或太阳的引力可分解为与地球引力平行和垂直的两个分量。前者因与强大的地球引力重合无所作为。后者不受地球引力的压制,是一个沿着地球表面的“横向”力。这个分量拉动海水,才是潮汐的真正起因。欧拉计算出月球对这个“潮汐力”(tidal force)的贡献是太阳的两倍多,纵然太阳对地球的引力远大于月球。
欧拉在巴塞尔大学时曾以一篇比较笛卡尔和牛顿的论文获取硕士学位。他的导师伯努利笃信笛卡尔,正以其学说论证地球是长球体。莫佩尔图在欧拉毕业离开两年后来到巴塞尔拜伯努利为师,掌握数学工具后却大力推广牛顿理论。到圣彼得堡后的欧拉数学技能更胜一筹。他纵横驰骋于传统的“数论”(number theory)和其它各个数学分支,在应邀解答趣味性的“柯尼斯堡七桥问题”1时开创“图论”(graph theory)。他将牛顿和莱布尼茨形异实同的新数学整合为规范的微积分,以简洁优美的形式重新表述牛顿的力学。今天物理学生熟悉的“牛顿方程”即出自欧拉之手。因此,欧拉不仅能举重若轻地洞察牛顿的疏漏,更在牛顿自己心有余而力不及处也成绩斐然。
第二次赢得法国科学院大奖的一年后,声名鹊起的欧拉在1741年应德国“大帝”弗里德里希二世(Frederick II)的盛情邀请离开陷入战乱的俄罗斯,迁至更接近欧洲文化中心的柏林。
弗里德里希二世也无比仰慕启蒙时代的巴黎。与圣彼得堡不同的是柏林早在十八世纪初就在莱布尼茨提议下有了普鲁士科学院,只是在其后几十年里碌碌无为。1740年代初,弗里德里希二世专门从巴黎请来莫佩尔图担任院长,改以法国学者为主体振兴科学院。他还指定论文必须以法语写就。普鲁士科学院和圣彼得堡科学院也都效仿法国科学院举行自己的征文大奖。欧拉在柏林不得不学法语,在完成弗里德里希二世指派的任务同时辅佐莫佩尔图管理科学院,并为两个后起的大奖担任评委等等。在忙得不亦乐乎之余,他还继续参加声望更高一筹的法国科学院征文。
1748年4月,欧拉收到法国数学家克莱罗(Alexis Clairaut)来信,告知他又得了奖。那是欧拉第五次赢得法国科学院大奖。克莱罗字里行间却流露出不屑。他说那年的来稿实在乏善可陈,只得矮子里拔将军。
克莱罗曾经跟随莫佩尔图远赴北极圈。在那个1740年代后期,前往南美测量赤道纬度间距的远征队员——包括曾在大奖赛中胜欧拉一筹的布格——在厄瓜多尔和秘鲁等地历经千难万险后陆续返国,带回更可靠的数据和难以置信的异国风情。他们的回忆录风行一时,激发民众对科学探险及地球外形争议的莫大兴趣。经由伏尔泰、莫佩尔图和埃米莉等人的启蒙、地球形状的证实和哈雷彗星在1758年底的回归,牛顿的理论终于在法国和欧洲落地生根。布丰、克莱罗和达朗贝尔(Jean-Baptiste le Rond d’Alembert)等新一代法国才俊与英国当年的牛顿、虎克、哈雷一样既合作又竞争,在摒弃笛卡尔衣钵同时追随牛顿实践笛卡尔以严谨数学进行逻辑推理的梦想。牛顿力学也是法国科学院大奖征文的热门选题和评判标准。欧拉赢得的1748年题目是土星和木星的运动,一个《原理》中未能完全解决的难题。
开普勒早已知道行星的运动并不严格符合他总结出的定律。牛顿从自己的原理出发推导出开普勒的定律,也为行星实际运行轨道与定律的偏差苦恼。正因为他的“万有引力”,行星不只是在太阳引力下运行,还会受到其它行星、卫星的引力干扰。轨道相邻的土星和木星质量最大,偏差尤为明显。距离太阳较近的木星公转速度是土星两倍多,每次“赶超”土星的前后都会引发二者轨道和速度的变动。这也是一个三体问题,与月球在地球引力下运动同时被太阳牵扯同出一辙。牛顿在多方探索后断定如此复杂的数学问题只能近似求解,却不得要领。
半个多世纪后,欧拉更为优越的微积分使得牛顿的先见有了实际的可能。行星和月球的运动的主体为分别以太阳或地球引力下的椭圆轨道。以此为本渐次加入其它行星或卫星引力的“微扰”(perturbation)修正可以逐步逼近真实的运动。在柏林的欧拉与在巴黎的克莱罗和达朗贝尔展开激烈的竞争,竭尽全力也没能成功。他们不得已地认定牛顿的引力定律不够完善,各自提出不同的修正方案争执不下。只有与欧拉同龄的布丰坚信牛顿,却没有足够数学能力参与这场高手对谈。
克莱罗便是对欧拉获奖论文中修正牛顿引力的方式不以为然。一年后,他高调宣布找出自己在微扰计算中的漏洞,改正后不再需要修正牛顿的引力。达朗贝尔随后也有了同样的突破。两人都对具体步骤守口如瓶。欧拉心急火燎,只好建议圣彼得堡科学院以月球轨道为题悬奖征文,诱惑克莱罗和达朗贝尔参赛。达朗贝尔没有上钩。欧拉作为评委还是如愿读到克莱罗的论文,在推荐克莱罗得奖同时发展出更为流畅的计算方法。牛顿的引力定律经受住严峻考验,无需修正。
新的计算方法足以相当准确地预测月球的未来行迹。远洋的海员可以通过以观测的月球方位查表获得所在的经度。那是伽利略、牛顿、哈雷等人的未竟之梦。可惜欧拉和依照他的方法计算、制作出月球位置表格的德国天文学家迈耶(Tobias Mayer)晚了一步。哈里森那时已经发明他的航海钟表,用之测算经度远比观察月球方便。即便如此,英国王家设立的解决经度难题大奖还是在其高达两万英镑的奖金里划出三千和三百英镑分别授予迈耶的遗孀和欧拉。
物理学家也从此有了应付三体问题的手段,尽管冗长繁复的计算令绝大多数人望而却步。
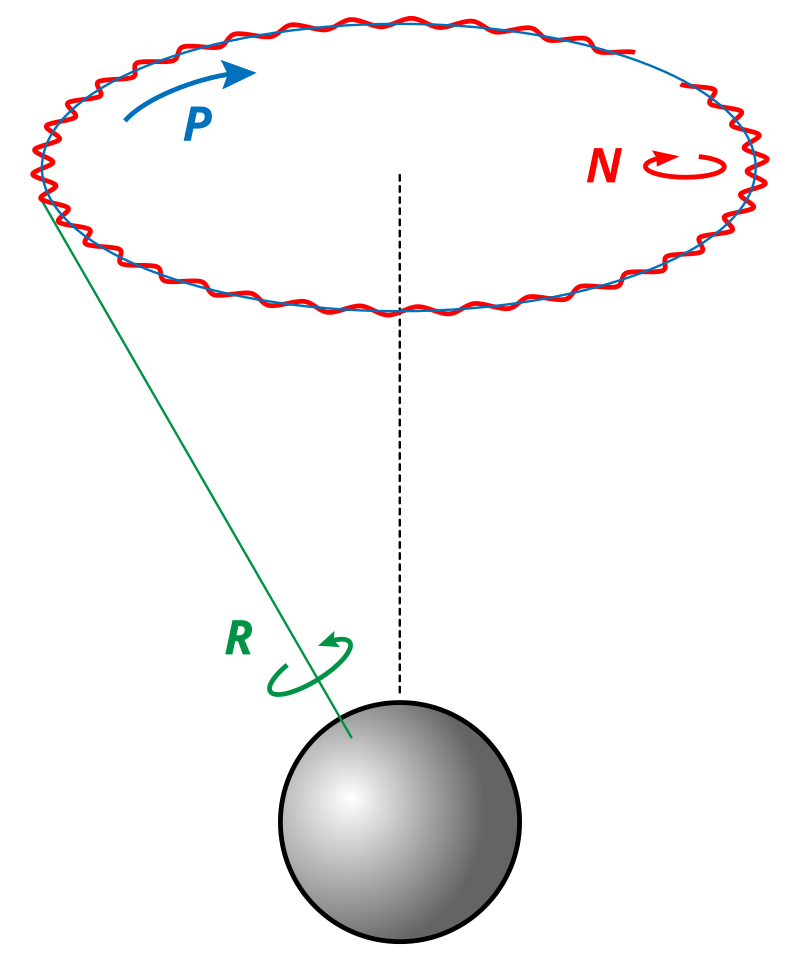
在茫茫宇宙之中,月球是地球最近的邻居、唯一的卫星。她也是太阳之外最能左右地球形态和运行的天体。这个三体问题曾最让牛顿头疼。他不仅洞悉地球上潮汐的发生源于天空中月球的引力,也为喜帕恰斯观察到的“等分日的提前”提供同样的解释:因为地球是一个扁球体,月球引力的力矩迫使地球的自转轴无法固定而旋转,造就一个周期长达两万七千年的“大年”。那是地球伴随着自转的进动,与日常的陀螺无异。
陀螺的运转经常不稳定,自转轴在沿圆周旋转(进动)时还会上下颠动。在牛顿逝世二十多年后的1748年,接替哈雷担任英国第三位王家天文学家的布拉德利(James Bradley)确认地球的自转轴在进动时也同样地起起伏伏,有一个18.6年的周期。他以拉丁语的“点头”将之命名为“章动”(nutation)。那是陀螺或球体自转、进动之外的第三个运动模式。人类脚底下的坚实大地在宇宙空间只是一个漂浮着的小小陀螺,在月球的扰动下摇摇摆摆。
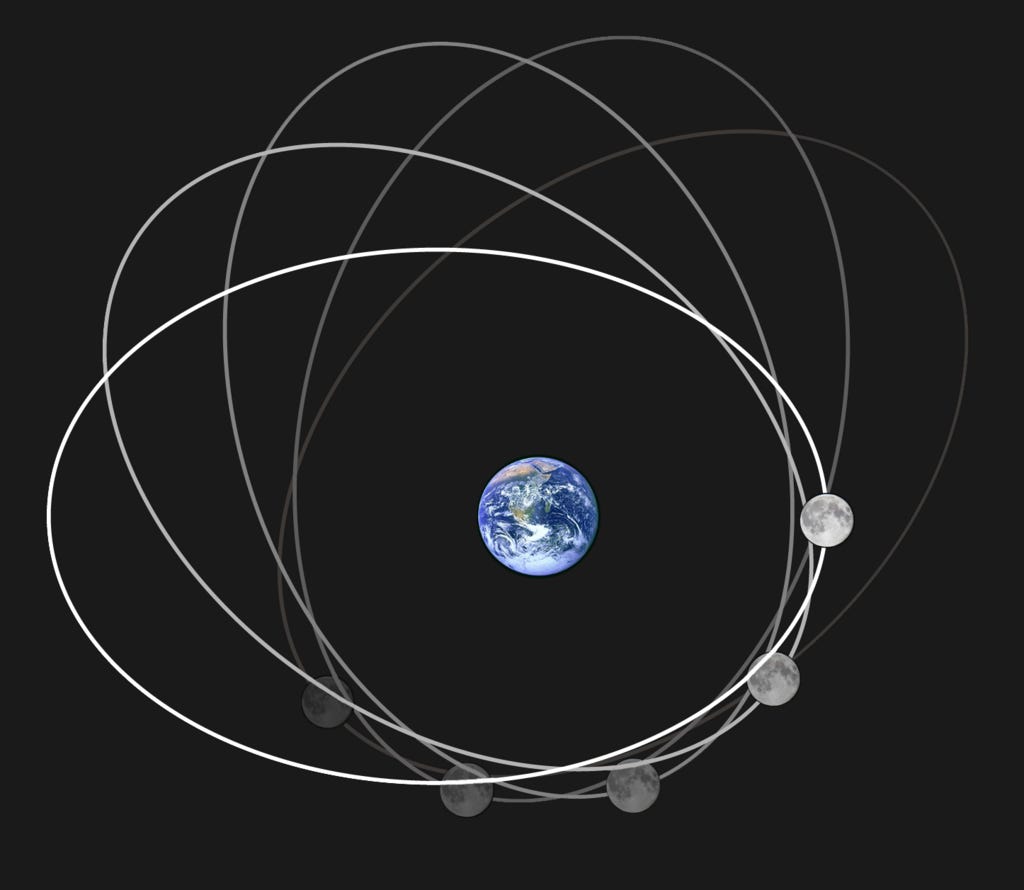
布拉德利和正在埋头计算月球轨道的欧拉等人不约而同地相信地球的章动也是月球引力之使然。因为太阳引力的扰动,月球绕太阳的公转不像开普勒定律描画地沿一个固定的椭圆兜圈。其近似椭圆的轨道没有闭合,本身也在绕地球转。那正是让克莱罗、达朗贝尔和欧拉绞尽脑汁的一个难点。
更有甚者,身为扁球体的地球以23.5度的倾角“斜躺”着一边自转一边绕太阳公转。月球又是在一个与地球公转轨道平面有着约5.1度夹角的平面上绕地球公转。三者的几何关系扑朔迷离,又时时刻刻处于变动之中。达朗贝尔率先从这盘根错节中脱颖而出,依据牛顿力学推导出月球驱使地球章动的力——或更准确而言,力矩。他的论文晦涩难懂,欧拉也读得满头雾水。好在欧拉理出其中头绪,以自己远为清晰的方式表述地球的章动。
那个年代的巴黎和柏林学者对此习以为常。才思敏捷的达朗贝尔行文杂乱无章,难以引起共鸣。而欧拉总能信手拈来,以简练的推导化“腐朽”为神奇。他也常常顺便地将成果据为己有。
江山代有才人出。欧拉在1755年也收到来自意大利的信,告知他的一些推导可以大为简化。信作者名叫拉格朗日(Joseph-Louis Lagrange),刚过十九岁。年近半百的欧拉善意地将后续论文压下,等年轻人公开成果后才发表。两人由此展开长久的合作。
十多年后,也是十九岁的拉普拉斯(Pierre-Simon Laplace)在1768年的巴黎敲响达朗贝尔的门。拉普拉斯在法国诺曼底乡村长大,只带有一封当地老师的介绍信。达朗贝尔不屑一顾,只让小青年回去自学,等有了自己的创见再来。他没想到拉普拉斯没等几天就又登门,交上一份关于牛顿力学的论文,捎带着推广了达朗贝尔自己的理论。达朗贝尔在震惊和欣赏之余接纳拉普拉斯,为他在巴黎的军事学院安排一份教职。2
岁月在更迭。莫佩尔图于1759年去世。已经在幕后替他履职多年的欧拉正式代理起普鲁士科学院院长的职责。可是弗里德里希二世更钟情高雅的法国贵族,一门心思争取达朗贝尔前来继任院长。欧拉于是再度远行,在1766年重返圣彼得堡,荣获叶卡捷琳娜大帝(Catherine the Great)的热情欢迎和极为优惠的待遇。在柏林的25年里,欧拉一直与圣彼得堡科学院保持紧密联系。当俄罗斯军队在1760年侵入柏林毁坏欧拉的府邸时,带队的将军当即为他道歉并巨款赔偿。叶卡捷琳娜大帝得知后也慷慨解囊加倍弥补。欧拉回圣彼得堡后更是宾至如归,硕果累累。他依然是法国科学院大奖赛的常客,创下参赛18次、获胜12次的个人记录。大奖题目每年在纯理论和实用性之间轮换,欧拉二者兼得,还曾连续三年蝉联获奖。
欧拉在1772年最后一次得奖时已是65岁高龄,因早年疾病后遗症双目失明。地球、月球、太阳纠缠不休的三体问题仍然在大奖赛中反复出现。两年前,欧拉与儿子一起在这个题目上拔得头筹。这一次,欧拉又是与拉格朗日共同得奖。哈雷晚年在格林威治天文台精心观测月球轨迹时察觉月球在莫名其妙地加速(secular acceleration),被法国科学院选作1772年的征文题。获奖的欧拉其实也没能找出月球加速的缘由,只猜测是弥漫宇宙的以太在推动。
拉格朗日那时已经由意大利移居柏林。在达朗贝尔表示不愿意离开巴黎后,弗里德里希二世干脆取消普鲁士科学院的院长职位。拉格朗日在欧拉和达朗贝尔的推荐下担任科学院的数学部主任,实际继承欧拉原有的位置。
孤身来到巴黎五年后,年仅24岁的拉普拉斯被接受为法国科学院成员。他在军事学院担负着繁重的教学任务,只能在闲暇时继续自己的研究。达朗贝尔为此致信拉格朗日,期望在普鲁士科学院为后起之秀找到更好的位置。拉普拉斯未能如愿以偿,但与比他大十三岁的拉格朗日开始长期的通信。他俩与长辈达朗贝尔和欧拉如出一辙地既密切协作又互不相让,承继以巴黎与柏林为轴心的学术纽带。
太阳系的行星运动井然有序,无疑为牛顿的引力和动力学定律的完美体现。然而“万有”的引力也不寻常。因为太阳的扰动,月球绕地球的轨道不是标准的闭合椭圆。同样地,地球和其它行星绕太阳公转的轨道也都时常偏离开普勒的定律。太阳系由太阳、地球、五大行星和它们各自数量不等的卫星组成,另外还经常有难以预料的彗星来来往往。所有星体两两之间均有引力,干扰彼此的运动。太阳系的既定秩序如何持续至今,又能维持多久不免令人疑惑。
人类生存的地球尤其显得弱不禁“风”,在小小月球的微扰中进动、章动不止。地球分别以24小时和365天为周期的自转和公转形成昼夜与春夏秋冬四季的更替,为芸芸众生特别是农作物创造良好的生存环境。稍有差错,后果也许不堪设想。
面对太阳系这一团乱麻般多体问题的牛顿在无奈中倒没有惶恐。他相信上帝为人类准备的家园不会自行分崩离析。欧拉亦有同感,认为太阳系会天经地义地保持自身稳定。后代的拉格朗日和拉普拉斯却诉诸于科学。他们协同努力,在欧拉奠定的基础上全面完善牛顿力学的严谨数学化和多体问题的微扰计算方法,证明太阳系的星球运动虽然曲折坎坷,也都不至于偏离开普勒的轨道太远而失控。人类的家园因此能够长久地保持其稳定性。
年轻的拉普拉斯也没忽视地球上由月球引力造成的潮汐。牛顿和欧拉对这一现象的解释都只是基于地球与月球及太阳相对方位的静态受力分析。拉普拉斯在1776年将其扩展为动力学,以一组微分方程3综合月球、太阳引力、地球的自转和海水的流动周密完整地描述潮汐。大约160年前,伽利略曾固执且错误地将潮汐完全归因于地球的自转。4拉普拉斯的分析表明欧拉所谓“横向”的潮汐力中的确包含地球自转成分,只是不及月球的引力。
拉普拉斯的动力学还捎带着解决一个被牛顿和欧拉忽视的细节。大潮在满月或新月——太阳、地球和月球三点成一线——时发生,但往往不与该天象同步,因地而异地有着几个小时到一两天的延迟。这在拉普拉斯的动力学里显而易见:海水在潮汐力拉动下沿地球表面的涌动是一个需要时间的过程。
从伽利略、牛顿到欧拉、拉普拉斯,人类经过四代人的努力才开始掌握潮汐这个司空见惯的自然现象。
1781年3月13日,在英国一个小镇定居的赫歇尔(William Herschel)从自制的天文望远镜里看到一个新亮点,以为又是一颗彗星来临。跟踪观察却显示那是一颗沿椭圆轨道运行的行星。这是人类远古时认识金、木、水、火、土五大行星的两千多年后第一次发现新的行星。5太阳系的领地随之被加倍,也变得更为复杂。
这颗“天王星”(Uranus)的露面又一次掀起计算行星轨道的热潮。拉普拉斯的微扰计算方法一枝独秀,成为学界标准。拉普拉斯也更为详尽地计算出地球与月球的轨道互动,解释让哈雷和欧拉茫然不解的月球加速现象。
当计算出的天王星轨道在六十年后与实际测量出现明显偏差时,天文学家认定那是另一颗未知行星在作祟,按图索骥地找到“海王星”(Neptune)。这是笛卡尔式的数学逻辑、牛顿的引力和动力学与欧拉和拉普拉斯的计算方法相结合的一大辉煌成就。
欧拉和达朗贝尔在1783年分别在圣彼得堡和巴黎去世。6拉普拉斯和以蒙日(Gaspard Monge)、勒让德(Adrien-Marie Legendre)等人为代表的更新一代正欣欣向荣,奠定巴黎欧洲数学中心地位。柏林的形势却急转直下。弗里德里希二世在1786年驾崩。继任的侄子抛弃他独尊法国传统,带领普鲁士科学院走向本土化。拉格朗日身为外人,又因妻子去世陷入极度抑郁。他接受法国国王、路易十四的五世孙路易十六(Louis XVI)的邀请离开柏林迁至巴黎。那是1787年,51岁的拉格朗日希望能在依然朝气蓬勃的新环境中重整旗鼓。
他不知道自己来到的是一个正值天翻地覆前夜的巴黎。
(待续)
Seven Bridges of Konigsberg
故事的另一版本是达朗贝尔交给拉普拉斯一本厚重的数学著作,惊奇地发现拉普拉斯在短短几天里掌握了书中内容。
即“拉普拉斯潮汐方程组”(Laplace tidal equations)
参阅《科学随笔:伽利略与浮体、潮汐及理性》。
其实从古希腊的喜帕恰斯到近代的弗拉姆斯蒂德、布拉德利和迈耶等天文学家都曾注意到过那个星点,可惜只将其错认为一颗黯淡的恒星。
相传拉普拉斯曾敬慕地宣称:“读欧拉,读欧拉。他是我们所有人的导师”(Read Euler; read Euler. He is the master of us all.),但这一引语只是后人假托之作。


这个系列写的真好,
真可以出一本书。