气候变迁背后的故事(十一)
彗星与化石
1726年5月,32岁的法国作家阿鲁埃(Francois-Marie Arouet)渡过海峡到伦敦避难。他常在作品中讽刺王公贵族,已经两度被囚禁于臭名昭著的巴士底狱。这一次,他在狱中求情,获准以流放代替坐牢。阿鲁埃这个名字乏人知晓,但英国人早已认识“伏尔泰”(Voltaire)。那是阿鲁埃八年前第一次坐牢后改的名。
虽然不过一水之隔,伏尔泰在伦敦大开眼界,看到一个与巴黎截然不同的社会。这里的言论、文化和商业均在自由环境里兴旺发达。他尤其羡慕王家学会成员们明目张胆地互相争辩,无所顾忌。在他的祖国,天主教会和皇权一如既往地无孔不入,整个国家死气沉沉。隶属皇室的法国科学院无时不在压制不合谐思想,即使内部有分歧也不能公之于众。伏尔泰抓住机会勤奋学习英语、遍访名流,全面考察英国的宗教、历史、政府和学界体制。躲过风头回国后,他将收获和体会以书信方式结集出版,向同胞介绍那个毗邻又陌生的国度。培根的方法、王家学会的运作和牛顿的思想都在这本《论英国人书简》1中占据一席之地。
那是《自然哲学的数学原理》问世四十年后。84岁高龄、深受膀胱结石折磨的牛顿在伏尔泰到来的七个月后离世。伦敦为牛顿举行隆重的葬礼,将遗体安葬于曾是王室专属的威斯敏斯特大教堂(Westminster Abbey)。伏尔泰亲身体验英国人对一位学者的尊重和仰慕,为之钦佩不已。他没见过牛顿,在听到牛顿侄女转述的牛顿看到苹果落地领悟万有引力故事后率先将之付诸文字。这个科学史传奇于是借伏尔泰的大名流传开来。在趣闻轶事之外,伏尔泰还在巴黎刻意结识数学家莫佩尔图(Pierre Maupertuis),虚心讨教《原理》中自己不甚了了的科学内容。
比伏尔泰年轻四岁的莫佩尔图是法国科学院正在崛起的新一代。他也是在旅居伦敦期间邂逅牛顿的《原理》,专程赴瑞士拜欧洲著名数学家伯努利(Johann Bernoulli)为师学习其中的数学。与欧洲主流一样,伯努利并不看好牛顿。他以精湛的数学严格证明笛卡尔的涡旋意味着一个长球体的地球,赢得1734年的法国科学院大奖。莫佩尔图在掌握数学技巧后却效仿牛顿“更爱真理”,针锋相对地证明自旋的星球必是扁球体。为躲避法国科学院的言论审查,他将论文送交王家学会的《哲学会刊》发表,绕过自家与之对应的《法国皇家科学院论文集》2。他的谨慎并非多余。1733年11月,继承父亲主持巴黎天文台的小卡西尼(Jacques Cassini)在巴黎附近沿着东西方向测量两条经线之间的距离,结果还是与地球作为长球体相吻合。伯努利的权威理论和卡西尼父子的多次测量一再巩固法国科学院的立场。他们确信地球是长球体,与牛顿预测相反。
莫佩尔图人微言轻,只能寄希望于更可靠的证据。那需要走出国门到遥远的北极和赤道附近实施大地测量。恰好法国海军对这一文人清谈发生浓厚兴趣,愿意提供资金实地勘测。他们期望从地球的真实形状能找到远洋航海的捷径。里歇去过的卡宴是法国唯一接近赤道的领地,却不具备大范围测量的地理环境。但在1731年时,法国与英国十多年的联盟破裂。敌对的西班牙摇身一变为法国的新盟友。西班牙在南美洲拥有大量殖民地,覆盖整个赤道地域。借助意外的天时地利,法国科学院在1735年组织远征队,在西班牙协同下奔赴今天的厄瓜多尔和秘鲁测量纬度间距。一年后,莫佩尔图也带队北上,前往今天瑞典与芬兰交界的托儿纳河谷(Torne Valley)进行同样的测量。
托儿纳河谷位于北极圈内,比当年皮西亚斯抵达的“终北之地”(冰岛)还略北一筹。但它在十八世纪初也已不再人迹罕至。莫佩尔图到那里后只用三个月完成测量任务,获得他早已预期的好消息:北极附近的纬度间距明显比在法国境内的长,表明地球是一个扁球体。
那时候,赴南美的远征队还在旅途中蹉跎,失去先机。他们随后历经热带气候、火山爆发、地震、战争等千难万险,直到1744年后才散兵游勇般陆续返回。好在这支远征队在赤道的测量比莫佩尔图的更为精细可靠,结果又相当一致:地球赤道处的半径与两极长179分之一,比牛顿估算的230分之一还更扁。他们还在南美的高山顶上、侧旁和山下分别测量摆钟的快慢,得到山体引力有与其质量成正比的数据。那是牛顿万有引力定律的第一个直接验证。摆钟也由此成为测量地球表面重力最原始、最简单的“重力仪”(gravimeter)。
这是人类历史上第一个由政府斥资组织、不同国家合作、跨越大半个地球的“大科学”项目。
远征队出发那年,伏尔泰的新剧《阿尔齐尔》3上演。那是他的宗教和爱情名剧《扎伊尔》4的翻版,但将故事改在西班牙统治下的秘鲁展开,以激发公众对那个遥远陌生地点的兴趣。因为《论英国人书简》中宣扬的自由、平等理念,伏尔泰那时已经陷入新的麻烦。他不得不逃出巴黎,躲到边远的夏特莱侯爵庄园避难。那里的侯爵夫人埃米莉(Emilie du Chatelet)是伏尔泰的长期情人。而更难得的是埃米莉也曾是莫佩尔图的学生兼情人,同样钟情于牛顿的科学。仰仗埃米莉和莫佩尔图的共同协助,伏尔泰在庄园里写出浅显易懂的《牛顿哲学要素》5,向法国大众普及来自异乡的科学思想。
埃米莉也独力完成《原理》的法语翻译,并为该书提供大量自己的注解和评论。可惜译著迟至埃米莉逝去七年后的1756年才得以出版。她在与伏尔泰和莫佩尔图分手后又有了新情人,在42岁时怀孕而不幸死于生产。
莫佩尔图等人在北极圈和赤道的大地测量、伏尔泰的《牛顿哲学要素》和埃米莉翻译的《原理》终于在十八世纪中后期冲破法国学界内外的思想桎梏,促使他们告别笛卡尔的教条而“皈依”承继笛卡尔思想的牛顿新学。那是牛顿去世的三十多年后。法国随之进入富有历史意义的“启蒙时代”(Age of Enlightenment)。
在1758年底,德国天文学家帕利奇(Georg Palitzsch)的望远镜总是对准夜空中一个特定的方向。终于,他在圣诞节之夜看到那里出现新的亮点。消息还未及传到法国时,那里的梅西耶(Charles Messier)也在1759年1月21日发现目标。他们都知道那又是一颗彗星的来临。
他们更知道,那是一颗彗星的又一次来临。
第谷、开普勒、伽利略、虎克、牛顿等几代英杰都亲眼目睹来无影去无踪的彗星。第谷和开普勒觉得彗星走的是直线,只是穿越太阳系的过客。年轻的虎克在1664年观察彗星时看出其轨迹也在弯曲,怀疑它是1618年一颗彗星的再现。法国的卡西尼也猜想那是第谷在1577年看到过的彗星。当1680年底和1681年初两颗彗星接连出现时,王家天文学家弗拉姆斯蒂德认定那是同一颗。因为彗星与太阳之间的磁力,彗星先被太阳吸引而来,后又遭受排斥反弹而去,故而它们的运行方向相反。牛顿对弗拉姆斯蒂的奇谈怪论嗤之以鼻,但仔细思量后也认可那是同一颗彗星。它们的一来一往其实是彗星在绕太阳公转,只在太阳背后时不得以见。牛顿由此肯定彗星与行星同样地遵从开普勒的定律。但能观察到彗星的时间太短暂,数据点不足以描画出彗星椭圆轨道的全貌。
作为《自然哲学的数学原理》出版人、编辑和排版制图技工,哈雷在牛顿每次送来书稿进展或修正时先睹为快。仗着近水楼台便利和自身的数学功底,他在牛顿之外最早掌握这个新理论,也跃跃欲试小试牛刀。诡秘的彗星自然地成为首选。哈雷为此花费多年功夫,逐步用牛顿建议的数值拟合方法还原出24颗彗星的轨道。虎克与卡西尼的的猜测都被证明为无稽之谈,但哈雷也确定弗拉姆斯蒂德在1682年观测的一颗彗星与开普勒在1607年观测的彗星轨道雷同,应该是同一颗。那颗彗星还在更早的1531年现过身,其轨道周期因而约为76年。那是一个又扁又大的椭圆。当时所知行星中距离太阳最远的是土星,轨道周期也还不到三十年。
哈雷于是信心十足地预测这颗彗星会在1758年再度归来,招呼天文学家拭目以待。当帕利奇和梅西耶看到星光如约而至时,他们的惊讶和激动充满对牛顿和哈雷的敬仰。那是牛顿力学第一个成功的预测,比解释开普勒定律更令人信服。有史以来第一次,彗星不再行迹莫测,降格为与日出日落无异的寻常。
已于1742年初离世的哈雷没能亲身体会辉煌的时刻。这颗并不是他发现的彗星被后人称作“哈雷彗星”,也属名至实归。自那时起,哈雷彗星忠实地每隔七十多年回访。距今最近的到来是在1986年,下一次则是2061年的后会有期。尽管如此,她的每次现身仍然会轰动一时,融合着大自然和人类智慧的双重神奇。
哈雷也在彗星的周期性中洞察更为实用的意义。从古老的晷针、日晷到伽利略的悬摆,大凡有固定周期性的自然现象都是现成的计时工具。晷针和日晷分别利用地球自转和公转计日计年。彗星长达几十年的公转周期则别具一格。因为被普遍看作凶兆,彗星的露面大多会在古书中留有详细记录,并与当时的变故紧密相连。根据彗星的已知周期性能够辨识出那些史籍所载的真实身份,从而判定历史事件的确切日子。我们现在知道,哈雷彗星在历史长河中“见证”过多次人类的战争和变故,甚至可能是《圣经》记载耶稣(Jesus)诞生时天边的“伯利恒之星”(Star of Bethlehem)。
不过彗星的轨道也很不稳定,每次进出太阳系时可能与某个行星“擦肩而过”而被其引力扰动。这在偶遇质量较大的木星和土星时尤为显著,是哈雷拟合彗星轨道时的遇到的最大困难。地球上看到的彗星回归周期也就不那么严格,作为历史的日历还有待更为精确的计算。哈雷没有灰心。他知道彗星之外还有很多引人注目的天文现象有同样的效用,包括更为震慑人心的日全食。1690年1月,哈雷在王家学会接连发表演讲,综合日全食、满月、海风、潮汐等自然因素论证古罗马凯撒(Julius Caesar)大帝入侵英伦的准确时间和登陆地点,将培根的经验主义方法引入历史研究范畴。
私下里,哈雷还向牛顿透露彗星不仅是历史事件的时间标记,还很可能身为始作俑者。受月球引力导致地球潮汐的启发,哈雷设想某颗彗星近距离掠过地球时的引力也应该能吸动海水造成超级涨潮。那也许是《圣经》里特大洪水的真实成因。他得到牛顿的回信首肯。但为了不得罪教会,哈雷将已经写好的论文压下没有发表。即使在英国,言论自由也有其既定界线。
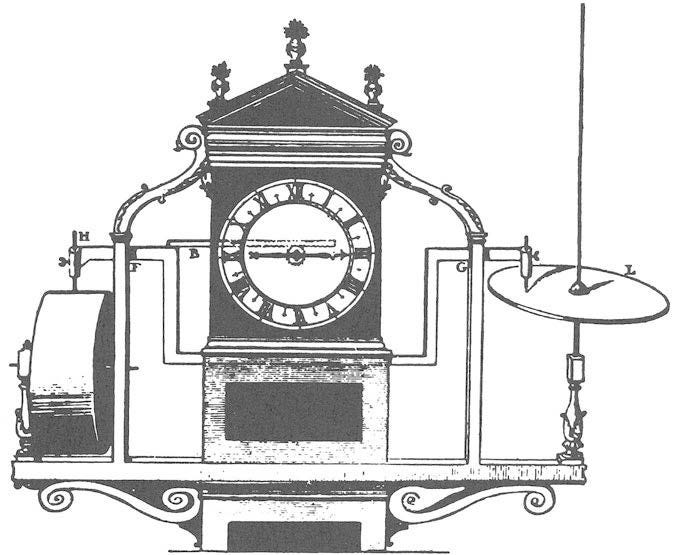
牛顿的《自然哲学的数学原理》出版时,虎克刚过半百之年。他在王家学会的薪金翻了一番,却也清楚地看到自己在英国学界的权威地位已经一去不复返。自协助波义耳制作气泵成名,虎克一直担任实验员,兢兢业业地完成学会交给的每一项任务,包括日常气象数据的采集和记录。1679年时,他在雷恩的建议下经过十多年的不懈努力成功创制“天气钟”(weather clock),用摆钟带动温度计、气压计、湿度计、风速计和雨量计,每隔十五分钟自动在纸带上记录读数。
这个异常繁复的机器不十分耐用,需要经常性的修理和调整。但它无疑是现代“气象仪”(meteorograph)的先声。
因为在引力优先权上与牛顿的争执,加之他俩昔日在光学等问题上的针锋相对,虎克的声誉正伴随着牛顿的如日中天一落千丈。《原理》问世的半年后,虎克钟爱的侄女因病去世。他一辈子单身,经常在日记里留下与各位保姆私通的暗记。这位侄女11岁时来到伦敦,在虎克的宠爱和抚养中长大。年满16岁后,她改以情人兼保姆的身份陪伴虎克整整十年。备受打击的虎克只得强打精神重整旗鼓,在学会里开办一个有关历史、气候和洪荒的系列公开讲座。他讲解的不是学术暮年的新见解,而是二十年前的旧话重提。那是他又一个被伦敦瘟疫和大火耽误的创见。
那时的虎克正值而立之年,因《显微图谱》的出版名噪一时。他在完成该书后曾回家乡怀特岛度假。与英格兰的海岸线相似,怀特岛上有很多高耸的临海悬崖,上面有看起来像是贝壳的“花纹石”(figured stones)。这类带有酷似动物或植物花纹的石块在世界各地都能被挖掘到,像磁石一样被认作有治病祛灾的神力。它们因此在拉丁文里叫做“挖掘所获”(fossil),即“化石”。虽然亚里士多德猜想那是活着的生物气息呼尽后的遗骸,人们还是将之看作没有什么特别意义的“自然界神奇”6。王家学会经常收到好事者送来的花纹石。虎克也曾用显微镜仔细观察,在《显微图谱》里展现它们的细节构造。他证实化石和贝壳的花纹没有区别,因而也认定化石是昔日的生命体。它们与也会时常被挖掘出的古代钱币、器皿等遗物同为往昔历史的印证。
问题是怀特岛的峭壁高出海面太多,上面不应该有贝壳生存。虎克亲自爬上去考察,发现那里不仅有贝壳,还有种类繁多的其它海洋生物化石。他砸开从高处坠落的大岩石,赫然看到坚硬的内层中居然也同样地丰富多彩。
回到伦敦,虎克在1667年第一次为这个现象开办系列讲座。他认为地球上的岩石、高山等并非亘古永恒,各有自己的演变历史。怀特岛甚至整个英伦三岛在过去的某个时刻完全浸没在水底,是海洋生物的乐园。它们在地质或地理变动中浮出水面后才逐步形成岩石与峭壁,因此其中会夹带着死去的动植物残骸。风雨、洪水、潮汐、地震、火山等等都可以是大变动的缘起,但这些时间短暂的事故不可能造就长时间、大规模的化石堆积。虎克于是想象地球在绕太阳公转、“横向”自转同时还有一个“纵向”的自转:表面的陆地缓慢地由赤道走向北极,再从北极走向赤道、南极……。欧洲大陆并不总是处在北极和赤道之间的北半球,在过去的“漂移”中也曾多次经受赤道的炎热和极地的酷寒,留有各种不同气候的烙印。
远早于牛顿,虎克那时已经指出地球是一个扁球体。不过他的地球还是有一个圆球形的固体内核,只是自由流动的海水在地球旋转的离心力作用下不再有圆球形的海平面。纵向的转动过于缓慢,离心力可忽略不计。造成昼夜交替的横向自转则促使赤道的海水比两极处深得多。或者说,赤道的海平面远比在两极的高。当欧洲在赤道一带经过时,怀特岛的峭壁和大陆的高山会全数被淹没在水下,直到过了那里的深渊后才缓缓露出。来不及逃亡的海洋生物这时永久地保留在山峰之巅。
这是虎克的“地球循环理论”(cyclic theory of earth)。崇山峻岭、江河湖海和芸芸众生都在赤道和极地的变更中一再历经这样的轮回。化石正是这一循环历史的忠实记录,却无法像彗星那样提供具体的时间印记。虎克还更进一层,推测某些物种不可避免地在这样的巨变中消亡殆尽,只以化石方式留存。在那翻天覆地之中,也可能会有新的物种诞生。
这也是一个纯粹出自演绎推理的理论,所依据的只有那些高崖上难以理解的化石。虎克知道他需要地球那个难以察觉的纵向自转的经验证据。他设计出一个简单而精巧的望远镜,希望通过很多年的跟踪测量判定一个地方的纬度的变化,即该地在地球的表面上的漂移。但这一切天方夜谭都在伦敦的两场大灾难中被遗忘。
二十多年后,虎克重新提起的地球循环理论仍然难以服众。他没能正面回答一个无可逃避的问题:地球有过足够的时间完成那缓慢的沧海桑田循环吗?
与哈雷在彗星导致大洪水思想中的犹豫相同,那是一个可能直接与《圣经》发生冲突的难题。
(待续)
Letters on the English
Memoirs of the Royal Academy of Sciences in Paris
Alzire
Zaire
Elements of the Philosophy of Newton
sports of nature